THE CONTACT LENS INDUSTRY is rapidly evolving, changing the way practitioners think about contact lens fitting. Consequently, the terminology used to define contact lens shape and fit is undergoing a similar evolution. Much of what we have learned in the last decade and a half in that regard comes from fitting scleral lenses, in which sagittal height—of both the cornea and the scleral lens—is key.
Although fitting by sagittal height is not new, awareness of this parameter has recently surged and is increasingly discussed with regard to other lens modalities, including rigid corneal lenses, orthokeratology (ortho-k) lenses, and even modern soft lenses. This movement is a return of soft lenses to their roots, given that their inventor, Otto Wichterle, first described them in terms of sagittal height in the late 1960s.
Metric System
The metric system is used frequently in optics and contact lens fitting—even in the myopia management arena, which arguably is the hottest topic right now. The most important eye measurements for myopia management are expressed in millimeters of axial eye length rather than dioptric values and refractive error.
For example, a normal eye has an axial length of about 23.5 mm, whereas an abnormal eye has an axial length greater than 26.0 mm and an increased risk of myopic retinopathy. Progression of myopia is measured annually in 0.1 mm steps, because for some age groups 0.1 mm is considered “normal” progression. However, it may be better to express these measurements in microns when they are less than 0.1 mm.
Moreover, research presented during the myopia session at the 2025 Global Specialty Lens Symposium indicated that measuring choroidal thickness (in microns) to assess short-term reaction to certain treatment options may be a viable way to assess the potential success of an intervention method. The choroid of highly myopic eyes is 111 ± 85 microns, which is significantly thinner compared to normal eyes at 263 ± 93 microns, and choroidal thickness can potentially be used to detect the risk of myopic macular degeneration.1,2
Although myopia management and higher-order aberrations are outside the scope of this article, it is interesting to mention that for the latter, the root mean square (RMS) value is also measured in microns. As an example, Hashemi and colleagues reported a mean higher-order Zernike RMS of 0.306 microns using a minimum pupil diameter of 5 mm for the normal eye.3
So, what is a micron again? Let’s zoom out for a second. Mount Hood in Oregon is 3.432 kilometers high; or you could say that it is 3,432 meters in height. In the metric system, the “step” from kilometer to meter, from meter to millimeter, and from millimeter to micron (micrometer, usually abbreviated as “micron” or the µm symbol) is the same; each step is 1/1000.
You can step up or step down the unit depending on the size of what you are measuring. For example, an increase in axial length of 50 microns would resonate better (especially with parents) than an increase of 0.05 mm, which could be perceived as quite marginal.
For small increments, which is the default in our contact lens industry and profession, the micron is the unit to use now. To put things in perspective, the human tear film (without a contact lens) is thought to be anywhere from 2 to 5 microns thick—which would be an inconvenient number of 0.002 to 0.005 if expressed in millimeters.4
Why the Metric System Makes Sense for Contact Lenses
The beauty of a height map when climbing a mountain is that you know exactly at what height you are and how much you have left to ascend. With a curvature map, you know that where it is “red,” it is going to be steep, but you could be at sea level or at 10,000 feet (or, in keeping with the metric system, 3,048 m); the curvature map does not tell you the height.
Increasingly, contact lenses are now described in terms of height rather than curvature. A typical scleral lens may have a height of 3.776 mm—or 3,776 microns. Scleral lens trial sets are often organized in steps based on microns of height. Microns are also used for thickness measurements related to contact lens fitting. For example, the fluid reservoir thickness (clearance) in scleral lens fitting is measured and recorded in microns.
As another example, the human corneal epithelial layer is 50 microns thick, and subtle changes applied to the epithelium by ortho-k lenses could slightly alter that thickness. A recent study from Spain reported the central average total corneal thickness to be 4.72 ± 1.04 microns thinner after ortho-k lenses were applied; the midperipheral corneal thickness was increased by 3.25 ± 1.60 microns.5
A molded soft lens with a power of –3.00 D on the ocular surface would have around 80 to 120 microns of central thickness (compared to a tear film thickness of only 2 to 5 microns), while the post-lens tear film in soft lens wear would be extremely thin (to just a few microns).4 Placing a soft lens on the eye seems quite invasive if you look at it from that perspective.
Rigid corneal lenses are somewhat thicker compared to soft lenses, and alterations in their design are measured in micron increments. Scleral lenses are even thicker but, obviously, they rest on the sclera (conjunctiva) rather than on the cornea.
Workbench: Ocular Surface Shape
To understand the use of large databases and corneal detection in contact lens fitting, let’s shift our attention to measuring the ocular surface using microns. Because here, too, subtle elevation differences in the “z-direction” (inward) can be detected using the sophisticated corneal topography technology that many of us have within reach.
Corneal topographers offer a wide range of options for analyzing the anterior surface of the eye. Industry encourages eyecare practitioners to lean on options that provide eye power or shape. For instance, the axial map displays corneal power and makes the connection between the anterior surface and vision. Another common topographical tool is the tangential map, which displays eye shape and helps us appreciate where the cornea is most and least curved. However, neither of these commonly used analysis displays communicate whether the ocular surface is high or low and by what magnitude.
This is where the elevation map becomes invaluable.6 This display is the only interpretation to communicate where a contact lens will land on the ocular surface and where it will lift. This is where microns become critically important to our appreciation of the ocular surface. Is it elevated or depressed, and by how much? Microns provide the measuring stick.
Height vs Elevation
Interestingly, height is not the same as elevation. In measuring ocular topography, ocular sagittal data is assessed by measuring the height of the eye across a defined diameter. By comparison, elevation is ideal for defining regional changes from 1 point of measure to the next.
In the real world, elevation changes along the course of a marathon could be used to rate the relative difficulty of the terrain that runners face. In ocular topography, elevation is used to appreciate high and low points on the ocular surface, which can help define the contact lens shape that would best fit these points of elevation or depression.
To appreciate this important topographical display, it is important to note that the elevation map uses a reference surface that is chosen to match the eye’s surface.7 In other words, the topography software analyzes the map, then finds the shape that most closely matches the surface.
Typically, the software selects a “best-fit sphere” (or alternative shape, like an ellipse) that aligns as similarly to the topography of the eye as possible. Then the software will display whether the tissue is above or below the reference surface in microns. Red or “hotter colors” indicate where the elevation of the eye is high compared to the best-fit sphere and, therefore, where a rigid contact lens will land or bear on the eye’s surface; the blue or cooler colors indicate where the eye surface is low in elevation and where a rigid contact lens will lift or allow for the pooling of tears (Figure 1).

Measuring in microns allows practitioners to appreciate the magnitude of elevation or depression on the eye’s surface. In a normal eye, the difference between the highest and lowest points may be measured in tens of microns of elevation change. In a keratoconus eye, the range could be measured in hundreds of microns (Figure 2).
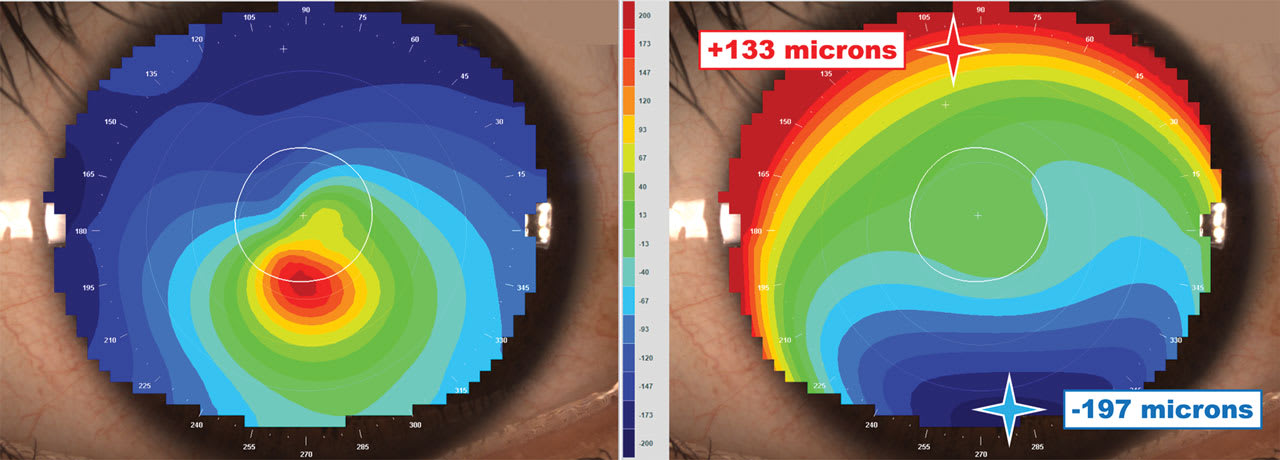
Our appreciation of the micron change in elevation across the eye’s surface facilitates the design of custom lenses that are precisely fitted from edge to edge. For instance, when a 30-micron depression is measured on the inferior cornea, the lens can be intuitively and easily adjusted by 30 microns to optimally fit the surface. By comparison, manipulating the various zones of a contact lens in radii is not as easy.
When to Choose a Back-Toric Corneal Lens
When fitting corneal and ortho-k lenses, it is important to assess eye symmetry or toricity. The relationship between corneal astigmatism and refractive cylinder is important. However, when we think about whether a symmetric or toric-landing lens is required, we are less concerned with the astigmatism of the central cornea and more focused on the difference in height in microns between the flat and steep meridians of the peripheral cornea.7
To make this assessment, a corneal topographer can be used to compare the height found in the flat and steep meridians at a given chord diameter, (eg, 8 mm). If the flat meridian measures 1,060 microns and the steep meridian measures 1,100 microns, the difference is 40 microns. A symmetric lens on this eye surface will land across the flat meridian but will have 40 microns of fluid under the steep meridian, which could cause the lens to be unstable, to decenter, and to reduce comfort.
Research indicates that toric-landing corneal or ortho-k lenses should be used when the depth difference between the meridians is more than 30 microns.8 Additional research indicates that the measured corneal astigmatism is less accurate for determining whether a symmetric or toric landing should be employed.9 Understanding the difference in elevation between the 2 principal meridians makes designing lenses more accurate (Figure 3).

Although scleral lenses have driven the recent industry use of microns to describe contact lens fittings, the first modern lens for which microns were routinely used across its entire surface was the reverse geometry ortho-k lens.
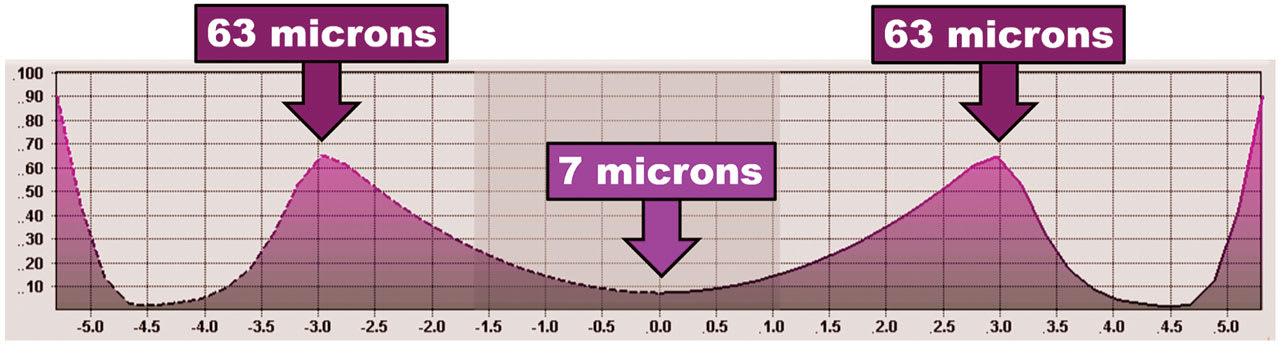
For example, most ortho-k lenses have approximately 7 microns of apical clearance.10 This tiny fluid layer between the lens and cornea is meant to protect the sensitive epithelium from lens bearing or rubbing. Additionally, the thin central fluid layer contrasts with the greater fluid thickness in the reservoir (Figure 4). The thin-to-thick ratio of fluid trapped between the lens and cornea is what produces the hydraulic forces that create the ortho-k effect on the epithelium.11
Outside the optical zone and the reverse zone is the alignment zone. This is the point where the lens is designed to touch down or land with 0 microns of vault.10 Of course, the lens rides on a layer of tears, but the zone with the least fluid thickness or vault would be the alignment zone (Figure 5).
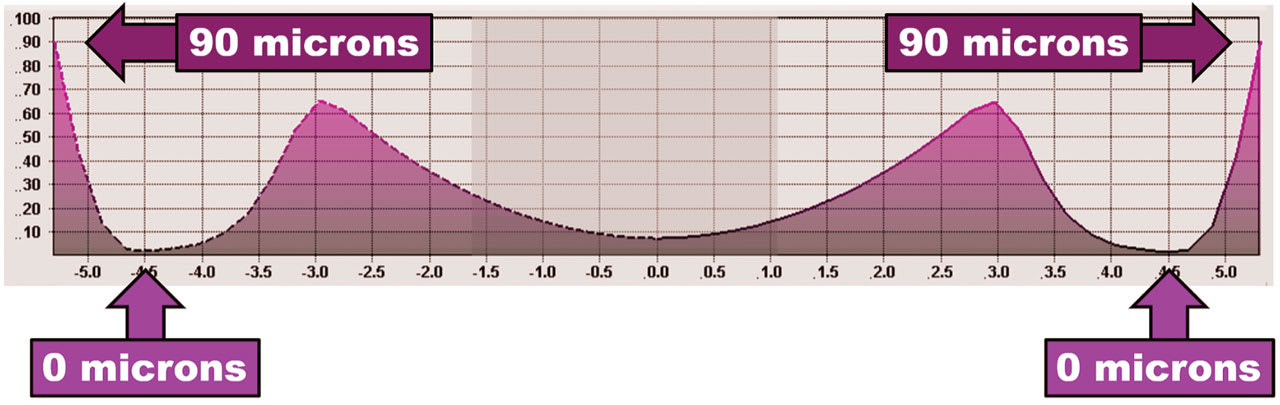
Finally, ortho-k—and essentially all corneal lenses—need to have edge clearance. This resembles the tip of a ski and encourages lens movement, tear exchange, comfort, and ease of lens removal. The micron clearance may vary by lens manufacturer, but typically it’s designed to exhibit 90 microns of fluid at the tip of the edge.10
Today, practitioners are able to use a topography-derived “free-form” design for corneal lenses, ortho-k, and scleral lenses. The topography can display the ocular surface as going up or down in microns and design a lens that follows the elevation, while also incorporating the correct micron thickness of fluid layer between the lens and the surface. When it comes to specialty contact lens fitting, it’s hard to imagine analyzing eye shape or designing lenses in anything but microns.
Scleral Lenses
One of the main questions when managing irregular astigmatism with contact lenses is: When is a rigid corneal lens or a scleral lens indicated? Either can be used, and both will help optically compensate for a patient’s irregular astigmatism due to their non-flexing nature.
One approach to help answer this question is to use corneal topography to predict whether the cornea is symmetric enough to support the physical fit of a rigid corneal contact lens. As previously mentioned, the elevation display of the corneal topography is the most predictive display of how a corneal lens will land and fit the cornea. In a study we peformed, the elevation map was analyzed along the meridian of greatest change at a chord of 8 mm. In the study, 100% of patients who had an elevation differential of more than 350 microns along that meridian were successfully fit with scleral lenses.11
Determining whether a cornea has enough symmetry to support the fit of a corneal contact lens is very useful in clinical practice. If the cornea’s elevation differential is above 350 microns, the recommendation is to choose a scleral lens that will be supported on the relatively more symmetric sclera, vaulting the highly irregular cornea entirely.
The study further showed that 96% of eyes with 0 to 100 microns of elevation difference and 94% of eyes with 101 to 200 microns of elevation difference were successfully fit with corneal lenses. However, only roughly 1 in 3 eyes with an elevation differential between 201 and 400 microns could be fit in corneal lenses. The authors concluded that eyes with less than 200 microns of elevation difference can confidently be fitted with corneal lenses, while eyes with more than 400 microns of elevation difference may require sclerals due to the increased corneal irregularity11 (Figure 6).

When to “Go Toric” With Scleral Lenses
When should scleral lenses be fit using toric landing zones? That is still a debate within the profession. One would guess that the elevation differential values are greater on the scleral portion of the ocular surface. Based on historical data, 1 study defined 300 microns of elevation difference (on a 16 mm concentric circle around the apex) as clinically significant.12 In a study on predicting dual-elevation scleral lens fitting, it was reported that the average dual sagittal depth difference was 263 microns, with a difference of 200 to 300 microns in 87.5% of eyes.13
Settling on Settling
When fitting a scleral lens, the next question is how much apical clearance, also referred to as fluid reservoir depth,14 is appropriate (Figure 7). This varies depending on the underlying corneal topography. Several researchers have attempted to identify how much a scleral lens settles as it is worn, and have shown that lenses tend to settle 30% to 40% of their initial clearance values.15,16 So if a scleral lens has an initial clearance of 250 microns centrally, it can be expected to settle 90 to 120 microns on average, leaving 180 to 210 microns of fluid reservoir in this example.

Fluid reservoir values for scleral lenses are typically measured in microns, as mentioned previously. Because many scleral lens fitting sets are organized by sagittal height measurements in microns, it is simple to adjust the clearance and select a second lens, if needed, to assess on-eye performance.
Soft Lens Fitting
Finally, microns and elevation are becoming increasingly considered in soft lens fitting also, as described in an article in the November/December 2024 issue of Contact Lens Spectrum titled “The Deep Learning Curve” (in which “deep” referred to elevation in microns as opposed to “steep” in reference to curvature in millimeters).17
Several instruments exist that can measure the ocular surface over the entire diameter of the landing zone area of a soft lens, including optical coherence tomography (OCT), Scheimpflug imaging, and profilometry. In addition, at least 2 corneal topographers can generate estimated height values of the cornea and can use the assumption that there is a tangential transition from peripheral cornea to anterior sclera (which is most often true) to calculate very reliable ocular sagittal height data (OC-SAG) over an area up to 15 mm in diameter.
Rubber Band
To conceptualize the factors involved in fitting a soft contact lens on the eye, visualize an elastic band stretched around the anterior ocular surface. Robert Mandell, OD, PhD, described this concept as early as 1974,18 and Graeme Young, MPhil, PhD, reintroduced it in the 1990s.19 It is a useful concept, as multiple factors influence the “tightness” or “rigidity” of this elastic band.
When fitting an elastic band around an object, it is essential to consider the shape and size of that object. Given that a soft contact lens typically has a diameter of 14.0 mm to 14.5 mm, understanding the ocular shape over that same diameter is crucial. This is significant because standard soft lenses generally fit well on average eyes. However, in cases of very flat or very deep eyes (high or low OC-SAG values), the fit may differ significantly.
The key is identifying normal eyes, which we call “Finding NEMOs” (normal eye measured ocular surfaces).20 Ideally, measurements should be taken across all meridians in a 360° fashion, as a solely horizontal measurement may deviate up to 200 microns from the vertical or other meridians.21
Soft Lens Tools
The counterpart to OC-SAG is CL-SAG—the sagittal depth of the soft lens. These values have been documented and published in recent years.22,23 Simply put, the higher the CL-SAG value, the deeper the lens and the greater its impact on the “elastic band” effect when all other parameters remain constant. Therefore, for flat eyes, selecting a lens with a lower CL-SAG value may be advisable, and vice versa.
Notably, deep lenses on flat eyes may feel comfortable at first but can cause problems with comfort and physiology at the end of the day.23 For accurate use of sagittal depth, CL-SAG values should be measured at 34°C (ocular temperature) rather than the ISO standard of 20°C, as temperature differences can result in discrepancies of 100 to 200 microns.24
What is increasingly clear is that base curve (BC) is not a very valuable parameter in soft lens fitting and in understanding soft lens behavior on-eye. As part of the Tear Film & Ocular Surface Society (TFOS) Dry Eye Workshop (DEWS), it was described as follows: “Base curve and diameter are surrogate measures for lens sag…increasing sag reduces movement and consequently improves comfort within the limits of acceptable fitting.”25 In general, a higher BC value will result in a flatter appearance, given the exact same lens design, diameter, eccentricity, material, etc. It is good to realize that when eyecare practitioners choose a flatter lens, they will in fact reduce the sagittal depth value of the lens—and that can alter the behavior of the lens on-eye (not so much flatter appearance of the lens, as such).
It should be noted that it has been shown that an “8.4 mm” of one lens type and manufacturer can be more than 400 microns different from an “8.4 mm” lens from another manufacturer (even different lens types from the same manufacturer can differ substantially).24 Awareness that base curve is not the only parameter that defines sagittal height can help when fitting custom soft lenses for patients who need these lens options.
Closing Remarks
In some parts of the world—the Netherlands is one of them—topography-based fitting has become the standard for rigid lenses, with an estimated 90% of all rigid corneal lenses fitted this way. This means that eyecare practitioners use corneal topography with applied software to design a lens themselves. Or, more commonly, they upload the topography to the manufacturer, and “the perfect” lens is designed using thousands of corneas in the manufacturer’s database as references.
For ortho-k lens fits, this estimate is even higher (close to 100%). So almost all ortho-k lenses in the Netherlands are “topography-based,” and trial sets are hardly used. Scleral lenses, assuming that correct anterior ocular surface shape data is available over a sufficient area, could go the same route; Scheimpflug, profilometry, and impression-based scleral lens fitting are quickly gaining popularity for scleral lenses.
Soft lenses, although flexible in nature and able to conform to the shape of the eye to a large degree, can be designed with a similar methodology—indeed leading to a new micron wave in contact lens fitting. Let’s move forward as a profession and elevate our thinking and dreaming to advance contact lens fitting to a higher level.
References
1. Shao L, Zhao H, Zhang R, Zhou W, Wei WB. Distribution and associated factors of choroidal thickness in highly myopic eyes—a real-world study based on a Chinese population. Eye (Lond). 2025;39(1):102-108. doi: 10.1038/s41433-024-03383-9
2. Liu R, Xuan M, Wang DC, et al. Using choroidal thickness to detect myopic macular degeneration. Int J Ophthalmol. 2024;17(2):317-323. doi: 10.18240/ijo.2024.02.14
3. Hashemi H, Khabazkhoob M, Jafarzadehpur E, et al. Higher order aberrations in a normal adult population. J Curr Ophthalmol. 2016;27(3-4):115-124. doi: 10.1016/j.joco.2015.11.002
4. Muntz A, Subbaraman LN, Sorbara L, Jones L. Tear exchange and contact lenses: a review. J Optom. 2015 Jan-Mar;8(1):2-11. doi: 10.1016/j.optom.2014.12.001
5. González-Pérez J, Sánchez-García A, Parafita MA. Epithelial and stromal thickness profile and lens decentration in myopic orthokeratology. J Optom. 2023;17(2):100485. doi: 10.1016/j.optom.2023.100485
6. Gatinel D, Malet J, Hoang-Xuan T, Azar DT. Corneal elevation topography: best fit sphere, elevation distance, asphericity, toricity, and clinical implications. Cornea. 2011;30(5):508-515. doi:10.1097/ICO.0b013e3181fb4fa7
7. Kojima R, Caroline P, Morrison S, Kinoshita B, Andre M, Lampa M. Should all orthokeratology lenses be toric? Poster presented at: Global Specialty Lens Symposium; January 2016; Las Vegas, NV.
8. Turpin S, Kojima R, Caroline P, Kinoshita B, Lampa M, Andre M. When is a toric orthokeratology lens design indicated? Poster presented at: Vision by Design; April 2018.
9. Kojima R, Kojima T, Heavyside N, et al. How Often Should We Prescribe Toric Orthokeratology Lenses? Poster presented at: Global Specialty Lens Symposium; January 2021; Las Vegas, NV.
10. Mountford J, Ruston D, Dave T. Orthokeratology – Principles and Practice. Butterworth Heinemann; 2004.
11. Zheng F, Caroline P, Kojima R, Kinoshita B, André M, Lampa M. Corneal Elevation Differences and the Initial Selection of Corneal and Scleral Contact Lens. Poster presented at: Global Specialty Lens Symposium; January 2015; Las Vegas, Nevada.
12. DeNaeyer G, Sanders DR, van der Worp E, Jedlicka J, Michaud L, Morrison S. Qualitative Assessment of Scleral Shape Patterns Using a New Wide Field Ocular Surface Elevation Topographer: The SSSG Study. J Cont Lens Res Sci. 2017;1(1):12-22. doi: 10.22374/jclrs.v1i1.11
13. Severinsky B, Shafi A. Predicting Dual-Elevation Scleral Lens Rotation Based on Front Corneal Elevation Map. Poster presented at: Global Specialty Lens Symposium; January 2024; Las Vegas, Nevada.
14. Michaud L, Lipson M, Kramer E, Walker M. The official guide to scleral lens terminology. Cont Lens Anterior Eye. 2020;43(6):529-534. doi: 10.1016/j.clae.2019.09.006
15. Otchere H, Jones LW, Sorbara L. Effect of Time on Scleral Lens Settling and Change in Corneal Clearance. Optom Vis Sci. 2017 Sep;94(9):908-913. doi: 10.1097/OPX.0000000000001111
16. Kauffman MJ, Gilmartin CA, Bennett ES, Bassi CJ. A Comparison of the Short-Term Settling of Three Scleral Lens Designs. Optom Vis Sci. 2014;91(9):1462-1466. doi: 10.1097/OPX.0000000000000409
17. Van der Worp E, Fujimoto M, Caroline C. The deep learning curve. Contact Lens Spectrum. 2024;39(9):10-17. clspectrum.com/issues/2024/novemberdecember/the-deep-learning-curve
18. Mandell R. Contact Lens Practice: Hard and Flexible Lenses. 2nd edition. Thomas; 1974.
19. Young G, Hall L, Sulley A, Osborn-Lorenz K, Wolffsohn JS. Inter-relationship of Soft Contact Lens Diameter, Base Curve Radius, and Fit. Optom Vis Sci. 2017;94(4):458-465. doi: 10.1097/OPX.0000000000001048
20. Van der Worp E. The science & skill of fitting a soft lens: an inconvenient truth. Contact Lens Spectrum - Special, Nov 2017.
21. Rojas, van der Worp E, Piñero. To analyze the differences of ocular sagittal height values (OC-SAG) in different meridians and in the 360 degrees. Poster presented at: Global Specialty Lens Symposium; January 18-21, 2024; Las Vegas, NV.
22. Van der Worp E, Mertz C. Sagittal height differences of frequent replacement silicone hydrogel contact lenses. Cont Lens Anterior Eye. 2015;38(3):157-162. doi: 10.1016/j.clae.2015.01.004
23. Andrew M, Zimmerman AT, Bailey MD. Contact lens adverse events and corneal sagittal depth. Cont Lens Anterior Eye. 2025 Jul;48(4):102413. doi: 10.1016/j.clae.2025.102413
24. Fujimoto MJ, van der Worp E, Kinoshita B, Lampa M, Coldrick BJ, Caroline P. Daily disposable soft lens sagittal depth and other lens parameter changes measured at room temperature (20°C) and on-eye temperature (34°C). Cont Lens Anterior Eye. 2024;47(3):102160. doi: 10.1016/j.clae.2024.102160
25. Stapleton F, Tan J. Impact of contact lens material, design, and fitting on discomfort. Eye Contact Lens. 2017;43(1):32-39. doi: 10.1097/ICL.0000000000000318




